urban teaching


urban teaching


(Note: a pdf file containing this essay is available here.)
My wife Ruth was a creative and highly regarded educator for 25 years before she took on a second career at about the time that I became a public-school teacher. Our conversations would go round and round. I would say “No child left behind” and she would say “One child at a time.” I would say “Learning standards” and she would say “Meet the child at the place of readiness.” Of course she was right every time. The conversations would stop when I said “How?” In this essay I offer an outline of one answer to “How?”
At the beginning of each year I started each of my three Geometry classes with a room of about 24 young people, many discouraged, many having had their mathematical development stunted before they entered high school, many with English skills that made the rate of acquisition of the required vocabulary a severe challenge in itself. From that starting point we began a wild ride, encountering and having to absorb a new lesson with a new set of concepts every two or three days, for about 150 class periods. By the end of the year a significant fraction of the students had fallen irretrievably behind, with others barely hanging on. Yet, by the time they became seniors, almost all of our students had passed the Massachusetts standard math test, and they graduated with a diploma.
Creating a math-literate person is like building a brick building: you do it one row at a time. Trying to skip steps is like trying to lay bricks on air. What’s bizarre is that we attempt it all the time and we can even believe that we’re succeeding sometimes. The source of our delusions is production quotas. It’s painful and perhaps unfair to draw this extreme analogy, but processing poorly prepared students through high school mathematics reminds me of the Soviet-era factories that met their five-year plans by building what they were told to build, even if nobody could use it.
If we’re going to do better we first need to identify the problem. As the person at the point of contact with—and the personal obligation to—the students, my take on the problem is this: I had been presented with a tragic dilemma. I had to fulfill two important yet conflicting mandates. Let us call these two mandates “The Material” and “The People.” The mandate we call The People is our duty as responsible teacher-citizens to help prepare all of our students for productive and fulfilling lives. The mandate we call The Material is our legal obligation to deliver a specified body of content within a specified time.
The public school political-legal environment has declared that The Material is the supreme value (the code word is accountability). This leads to a delivery strategy I shall call “Material First.” The logic of Material First is that if we can deliver the content successfully then the students will be well on their ways, and we will have therefore also performed The People.
Given the classroom scenario I describe above, it doesn’t seem to work that way, because the assumption within the logic of Material First isn’t true. My efforts to deliver the specified body of content in the specified time routinely generated hundreds of missed opportunities for my students to experience the day-to-day successes they needed so badly in order to have a more general success. In fact, neither The Material nor The People was being at all well performed. Yet we were making our numbers, more or less, so the reality was being masked.
Meanwhile, what are the meta-educators doing? When I learn about the research in mathematics education that is going on in colleges of education, I see exciting and interesting work, almost all of it with young children. The education strategy inherent in this research seems to be: if the teacher deeply understands the underlying mathematics and uses that understanding strategically while applying the teaching techniques being developed, he or she should focus on eliciting the daily classroom successes of the students, and the learning will occur. It is a wonderfully optimistic idea, based on repeated observations that, given the right learning environment, children will learn.
My students, however, arrive at my classroom bearing experiential baggage that obviously differs between primary and secondary students. My observations of my students were not consistent with these repeated observations of young children.
As educators we carry an article of faith that, given the right environment, the students I have described above will indeed learn what is put in front of them. Clearly, then, our task is to find the right learning environment for them. The knot we have not figured out how to unravel is how to do this within the Material First mandate.
I shall propose an alternative strategy for delivering our services. To distinguish it from Material First I shall call the alternative strategy Bounded Preparation First. The following table compares these two strategies.
In order to meet the needs of the students with whom I am familiar, in the course with which I am familiar (high school Geometry taught in grade 10) I foresee dividing the total curriculum time equally between preparation and content delivery. Stated another way, I am suggesting that it might well be necessary to reduce by half the size of the body of content to be delivered.
Immediately two important questions arise.
1.What makes it possible to believe that the Bounded Preparation First strategy would be any kind of an improvement?
2.Given a satisfactory answer to the first question, what will be going on in the classroom differently that will make Bounded Preparation First work?
What makes me believe that the Bounded Preparation First strategy will in fact lead to improved student performance is my intimate familiarity with the great inefficiency of the present method. Here is the essence of this proposal: within the suggested limit of a half year, a greater bottom-line student performance improvement can be obtained per class hour by addressing this inefficiency than by addressing the content delivery process.
At a gross level, here are the characteristics of this inefficiency that must be addressed by the preparation process.
1.Virtually all of my students arrive with no understanding of working in teams. They have neither expectations nor skills for working together in order to work more effectively. I have experimented extensively with attempting to create team problem-solving environments in my classes, and I have concluded that what is arguably the most important workplace skill that can be given to high school students, the ability to create and work together in teams, has been almost completely ignored. Yet working in teams is a seriously under-exploited technique for success in high school, since the students can often learn better from each other in small groups than they do from the teacher.
2.Most of my students arrive with no appreciation for the importance to them of using their learning time to the best of their abilities. There are known motivational techniques for dealing with this common side-effect of adolescence, but it seems not to have occurred to many people that these techniques have a direct application in the mathematics classroom.
3.Most of my students arrive with varying, often unsatisfactory, skills for attacking and overcoming unfamiliar content that must be learned. For whatever reason, many are not willing and/or prepared to persist in an effort to overcome new material.
4.Most of my students arrive with varying, often major, gaps in their mathematical preparation, gaps that must be filled for them to be able to absorb the course content.
It is no accident that, of these four issues, only one is related to math preparation; the other three relate to effective socialization and personal discipline. The socialization and discipline deficits of many students make any attempt to deliver difficult new knowledge grossly inefficient.
Much progress is possible toward remediation of these deficits, provided that the teacher and students cooperate in creating an affirmative learning community within the classroom. My experiments in my MCAS classes, where I had control over the balance between community-building and content, have given me confidence that this is possible with almost all students; this is where much of that freed-up class time should go.
Having stated all this I am not prepared to assert that any of us know how to create reliably such an affirmative learning community in an environment where resistance is the norm. But I am prepared to assert that this is how we should be using our professional development resources.
* * *
Now I shall present a simple numeric model that supports the assertion that, using the form and scoring method of the MCAS math test, a good knowledge of half of the course content can lead to a score near the bottom of the Proficient range.
In the fall of 2003 I wrote a paper for my students that explained the structure and scoring method of the MCAS test. You can see the paper by clicking here. Following is a brief summary.
Scoring the math MCAS test leads to a “raw score” in the range 0 to 60. The test has three kinds of “items” (questions), in a total of 42 items:
1.There are 32 multiple-choice items, each with four choices given. Each multiple-choice item receives a score of 1 if it is answered correctly and a score of 0 if it is answered incorrectly or not answered at all. The multiple-choice items contribute 32 of the possible 60 total points of the raw score.
2.There are 4 short-answer items, which ask the student to write a short answer in a box on the answer document. Each of these items receives a score of 1 if answered correctly, 0 otherwise. The short-answer items contribute 4 of the possible 60 total points of the raw score.
3.There are 6 open-response items. Each open-response item has several parts that progressively discuss a single mathematics problem. Each open-response item can receive a score between 0 and 4, according to well-documented criteria (unknown to the student) in which the scorers are trained. The open-response items contribute 24 of the possible 60 total points of the raw score.
During the four years I was teaching the threshold for passing ranged between 19 and the mid-20s, depending on the difficulty of the test. Notice that an expected score of 20 can be reached by getting a 2 on each open-response item (this is within reach with a competent partial answer) and answering all the multiple-choice items randomly. Since every student knows the answer to at least a few multiple-choice items, and some students are able to rule out two choices of a few multiple-choice items they don’t know and then do the equivalent of flipping a coin, the test hasn’t been difficult to pass. This suggests that the bar was actually set pretty low. (I understood before I left that the bar was soon to be raised radically.)
The model I show here quantifies this reasoning. In the model the independent variable is f, the “fraction of knowledge,” expressed as a fraction between 0 and 1 or as a percentage between 0 and 100. Assigning a value to f divides the test into two portions: the portion the student knows and the portion the student doesn’t know. (If f = 0 the whole test is the unknown portion; if f = 50% half the test is known and half is unknown.) In scoring according to this model, the student is assumed to do B work on the known portion and F work on the unknown portion. For multiple-choice items, B work means all the items in the known portion are answered correctly (1 point per item) and F work means that one quarter of the items in the unknown portion are answered correctly (the result of random choice). For short-answer items, B work means all the items in the known portion are answered correctly (1 point per item) and F work means that all the items in the unknown portion are answered incorrectly. For open-response items, B work means that all the items in the known portion receive 3 points; F work means that half the items in the unknown portion receive 1 point.
This is a continuous model that leads to fractional scores, but since it is not meant to be rigorously predictive, that should be of no concern.
The following chart shows how the raw score varies as a function of f, the fraction of knowledge.
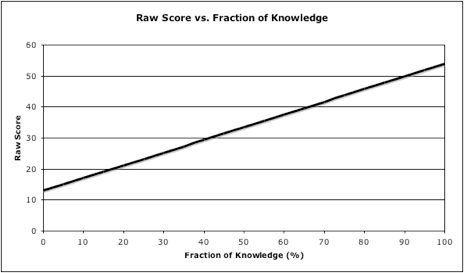
Since historically a raw score in the mid-20s was passing and a raw score in the mid-30s was (close to) proficient, this model suggests that a “Needs Improvement” (but, at present, passing) score is achievable with 25% knowledge, and 50% knowledge is near Proficient. This model therefore gives some credence to the assertion that if the students learn well one half of the material on which they will be tested, their work will be considered proficient. I am persuaded that this will be an improvement over current practice for many, perhaps most, students in the math classes I have known.
* * *
One point of creating an affirmative learning community in the classroom is that the students will indeed learn well the assigned half of the total content. An arguably more important benefit is that the students will have learned a life lesson they will carry with them far beyond the mathematics classroom. Bounded Preparation First can turn Material First upside-down: finding, and using well, the right mix of valuable class-time resources between content delivery and creating an affirmative learning culture in the classroom will put the students first—where they belong—and will assure satisfactory performance of our content delivery mandates.
© Copyright 2008 Mel Conway PhD
A Radical Proposal
Monday, March 10, 2008
